算法概论实验十一

发表于 | 分类于 
1
2
3
4
5
6
7
8
9
10
11
12
13
实验十一

实验目的与要求：
（1）	掌握对无向图的2-连通分量的划分算法。
（2）	理解与掌握在含负权值边的图中求最短路径问题的算法。

1．无向图的双连通分量问题
【问题描述】
给定一个无向图，设计一个算法，判断该图中是否存在关节点，并划分双连通分量。

2．带负权值边的有向图中的最短路径路径问题
【问题描述】
对于一个带负权值边的有向图，实现Bellman-Ford算法，求出从指定顶点s到其余顶点的最短路径，并判断图中是否存在负环。

#1．无向图的双连通分量问题

##1.1结构化定义

1
2
3
4
5
6
7
8
9
10
11
//为了方便输出双联通分量，定义一个结构
struct myedge
{
	int start;
	int end;
	myedge(int a, int b)
	{
		start = a;
		end = b;
	}
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

template<class T>
class MGraph
{
public:
	MGraph(T v[], int n, int e);//无向图的邻接矩阵建立
	MGraph();
	virtual ~MGraph();
	void Print();//打印图
	void print_prepost();//打印prepostback表
	int BiDFS(int v);//关节点
private:
	int vexnum, edgenum;	//vexnum--顶点数 edgenum--边数
	vector<vector<int> > edges;   //邻接矩阵 
	vector<vector<bool> > edges_view;   //领街边判定表
	vector<T> vexs;			//顶点表
	vector<int> pre; 
	vector<int> post;
	vector<int> back;
	vector<int> vex_cnt;  //输出辅助计数器
	stack<myedge> edgeStack;//边集存储
	int clock;
	int gettruenum();	//获取判断表中true数量
	bool getVexV(int v);//判断是否存在未访问边
	myedge getFirstVw(int v);//找到vw边
	vector<vector<int>> show_edge;
};

##1.2 关键函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
//Bicomponent Algorithm 
template<class T>
int MGraph<T>::BiDFS(int v)
{
	pre[v] = clock;
	clock++;
	back[v] = pre[v];
	while (getVexV(v))
	{
		myedge t = getFirstVw(v);
		edgeStack.push(t);
		vex_cnt[t.start]++;//辅助保存start出现次数
		if (pre[t.end] == -1)//如果是tree边
		{
			int wBack = BiDFS(t.end);
			if (wBack >= pre[v])
			{
				cout << "双连通分量:" << endl;
				int tmp = edgeStack.top().end;
				if (vex_cnt[tmp] > 0)
				{
					while (edgeStack.top().start != tmp)
					{
						cout << vexs[edgeStack.top().start] << "->" << vexs[edgeStack.top().end] << endl;
						vex_cnt[edgeStack.top().start]--;
						edgeStack.pop();
					}

				}
				cout << vexs[edgeStack.top().start] << "->" << vexs[edgeStack.top().end] << endl;
				vex_cnt[edgeStack.top().start]--;
				edgeStack.pop();
			}
			back[v] = min(back[v], wBack);
		}
		else
		{
			back[v] = min(pre[t.end], back[v]);
		}
	}
	post[v] = clock;
	clock++;
	return back[v];
}

##1.3 测试函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int main()
{
	//char a[] = { '1', '2', '3', '4', '5','6','7','8' };
	char a[] = { 'A', 'B', 'C', 'D', 'E','F','G','H','I','J' };
	MGraph<char> m(a, 10, 14);
	cout << endl << "打印测试：" << endl;
	m.Print();

	cout << endl << "关节点测试测试：" << endl;
	m.BiDFS(9);
	cout << endl;

	cout << "pre/post/back值测试：\n";
	m.print_prepost();

	return 0;
}

##1.4 测试截图
1.png-14.7kB

#2理解与掌握在含负权值边的图中求最短路径问题的算法
简单，易理解 从源点出发，做V-1次大循环，每次对所有边进行松弛更新

##2.1BellmanFord

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
template <class T>
bool MGraph<T>::BellmanFord(int source)
{
	dist[source] = 0;

	for (int i = 1; i <= vexnum - 1; i++)
	{
		for (int u = 0; u < vexnum;u++)
		{
			for (int v = 0; v<vexnum;v++)
			{
				if (edges_view[u][v]==true)
				{
					update(u, v, edges[u][v]);
				}
			}
		}
	}

	// 判断是否有负环路
	for (int u = 0; u < vexnum; u++)
	{
		for (int v = 0; v < vexnum; v++)
		{
			if (edges_view[u][v] == true)
			{
				if (dist[v] > dist[u] + edges[u][v])
				{
					return false;
				}
			}
		}
	}
	return true;
}

##2.2更新

1
2
3
4
5
6
template <class T>
void MGraph<T>::update(int u, int v, int weight)
{
	if (dist[v] > dist[u] + weight)
		dist[v] = dist[u] + weight;
}

##2.3测试函数

1
2
3
4
5
6
7
8
9
10
11
int main()
{
	//char a[] = { 's', '2', '3', '4', '5','6','7','t' };
	//char a[] = { 'A', 'B', 'C', 'D', 'E','F','G','H','I','J' };
	char a[] = { 'A', 'B', 'C', 'D', 'E'};
	MGraph<char> m(a, 5, 8);
	cout << endl << "打印测试：" << endl;
	m.Print();
	m.Print_dist(1);
	return 0;
}

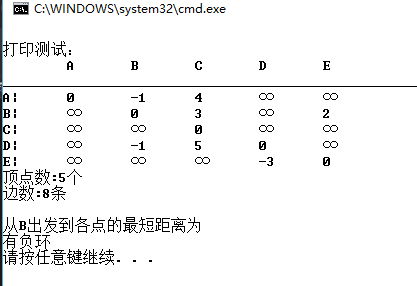
##2.4测试截图
2.png-9.6kB
3.png-14.3kB