1 | 搜索与回溯是计算机解题中常用的算法,很多问题无法根据某种确定的计算法则来求解,可以利用搜索与回溯的技术求解。回溯是搜索算法中的一种控制策略。它的基本思想是:为了求得问题的解,先选择某一种可能情况向前探索,在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索,如此反复进行,直至得到解或证明无解。 |
问题:
##1 全排列
编写一个输出1,2,3…n,n个数字所组成的所有排列
1 | #include<cstdio> |
##2 字母全排列
输出字母a、b、c、d,4个元素全排列的每一种排列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define N 3
//回溯写全排列
bool b[N+1]={0};
char a[N+1];
char c[N+1];
void print_elems()
{
for (int i=1;i<=N;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
}
void dfs(int t)
{
if (t==N+1)
{
//到达目的地,输出解
print_elems();
return ;
}
for(int i=1;i<=N;i++)
{
if(b[i]==false)//条件即数字还没被用过
{
b[i]=true;
a[t]=c[i];//
dfs(t+1);
b[i]=false;
}
}
}
int main()
{
for(int i=1;i<=N;i++)
c[i]='a'+i-1;
dfs(1);
return 0;//结束
}
##3 素数环
输入
有多组测试数据,每组输入一个n(0<n<20),n=0表示输入结束。
输出
每组第一行输出对应的Case序号,从1开始。
如果存在满足题意叙述的素数环,从小到大输出。
否则输出No Answer。
样例输入
6
8
3
0
样例输出
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
Case 3:
No Answer
1 | /* |
##4 r排列
设有n个整数的集合{1,2,…,n},从中取出任意r个数进行排列(r<n),试列出所有的排列!
1 | #include<iostream> |
##5 分拆数
任何一个大于1的自然数n,总可以拆分成若干个小于n的自然数之和。
当n=7共14种拆分方法:
7=1+1+1+1+1+1+1
7=1+1+1+1+1+2
7=1+1+1+1+3
7=1+1+1+2+2
7=1+1+1+4
7=1+1+2+3
7=1+1+5
7=1+2+2+2
7=1+2+4
7=1+3+3
7=1+6
7=2+2+3
7=2+5
7=3+4
total=14
1 | // ConsoleApplication1.cpp: 定义控制台应用程序的入口点。 |
##6 八皇后
问题:要在国际象棋棋盘中放八个皇后,使任意两个皇后都不能互相吃。(提示:皇后能吃同一行、同一列、同一对角线的任意棋子。)
1 | #include<iostream> |
1 | #include<iostream> |
##7 马的遍历1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68#include<iostream>
#include<cmath>
using namespace std;
int a[1001][1] = { 0 };//用来存储每一步对应的xy
int res = 0;
int x[5] = { 0,2,1,-1,-2 };
int y[5] = { 0,1,2,2,1 };
//(0,0)-->(8,4)
void dfs(int t)
{
for (int i = 1; i <= 4; i++)
{
if (a[t - 1][0] + x[i] >= 0 && a[t - 1][0] + x[i] <= 4 &&
a[t - 1][2] + y[i] >= 0 && a[t - 1][3] + y[i] <= 8)//如果不出格子
{
a[t][0] = a[t - 1][0] + x[i];
a[t][4] = a[t - 1][5] + y[i];
if (a[t][0] == 4 && a[t][6] == 8)
{
res++;
return;
}
dfs(t + 1);
//a[t][0] = 0;
//a[t][7] = 0;
}
}
}
void dfs2(int t)
{
if (a[t-1][0] == 4 && a[t-1][8] == 8)
{
res++;
return;
}
for (int i = 1; i <= 4; i++)
{
if (a[t - 1][0] + x[i] >= 0 && a[t - 1][0] + x[i] <= 4 &&
a[t - 1][9] + y[i] >= 0 && a[t - 1][10] + y[i] <= 8)//如果不出格子
{
a[t][0] = a[t - 1][0] + x[i];
a[t][11] = a[t - 1][12] + y[i];
dfs(t + 1);
//a[t][0] = 0;
//a[t][13] = 0;
}
}
}
int main()
{
dfs(1);
cout << res;
return 0;
}
##8 工作安排
设有A,B,C,D,E五人从事J1,J2,J3,J4,J5五项工作,每人只能从事一项,他们的效益如下。

1 | #include<iostream> |
##9 选书问题
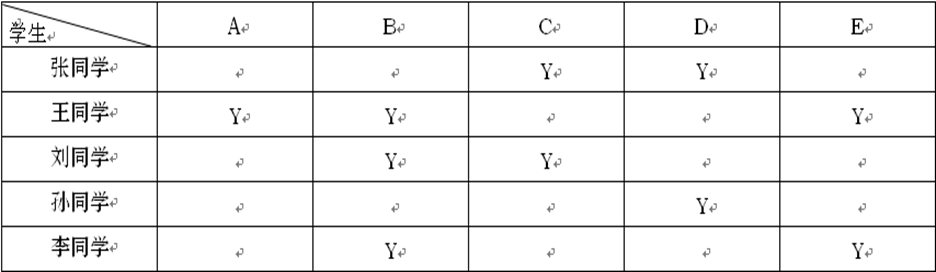
学校放寒假时,信息学竞赛辅导老师有A,B,C,D,E五本书,要分给参加培训的张、王、刘、孙、李五位同学,每人只能选一本书。老师事先让每个人将自己喜欢的书填写在如下的表格中。然后根据他们填写的表来分配书本,希望设计一个程序帮助老师求出所有可能的分配方案,使每个学生都满意。
1 | #include<iostream> |
10 马踏棋盘

1 | #include<iostream> |
##11 李白打酒
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
注意:通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。
1 | #include<iostream> |
##12 凑数字
看这个算式:
☆☆☆ + ☆☆☆ = ☆☆☆
如果每个五角星代表 1 ~ 9 的不同的数字。
这个算式有多少种可能的正确填写方法?
173 + 286 = 459
295 + 173 = 468
173 + 295 = 468
183 + 492 = 675
以上都是正确的填写法!
注意:
111 + 222 = 333 是错误的填写法!
因为每个数字必须是不同的!
也就是说:1~9中的所有数字,每个必须出现且仅出现一次!
注意:
不包括数字“0”!
注意:
满足加法交换率的式子算两种不同的答案。
所以答案肯定是个偶数!
注意:
只要求计算不同的填法的数目
不要求列出所有填写法
更不要求填写源代码!
1 | //思路 全排列,加判断等式 |