1 | 实验四 |
#1.多段图中的最短路径问题1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36#include<iostream>
#include<cmath>
#include<string.h>
using namespace std;
int dp[1222222],alone[1222222],a[1222222];
int main()
{
int i,j,n,m;
while(~scanf("%d",&m))
{
scanf("%d",&n);
memset(dp,0,sizeof(dp));
memset(alone ,0,sizeof(alone));
for(i=1;i<=n;i++)scanf("%d",&a[i]);
int tmax;
for(i=1;i<=m;i++)//★分i段
{
tmax=-(1<<30);
for(j=i;j<=n;j++)
{
dp[j]=_cpp_max(dp[j-1],alone[j-1])+a[j];
printf("%2d %2d %2d\n",a[j],alone[j-1],dp[j]);
if(j>i)alone[j-1]=tmax;
if(tmax<dp[j])tmax=dp[j];
}
}
printf("%d\n",tmax);
}
return 0;
}
#2.有向无环图中的最短路径问题1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96#include <iostream>
#include <limits.h>
using namespace std;
void Init_Graph(int N,int **S)
{
int i,j;
cout<<"输入边的长度:输入1 2 4 表示点1 与 2的边的长度为 4:首数字为0表示结束输入"<<endl;
cin>>i;
while(i!=0)
{
cin>>j;
cin>>S[i][j];
cin>>i;
}
}
void DP(int N,int **S,int *dist,int *from)
{
int i,j;
for(j=0;j<N+1;j++)
{
if(S[1][j]<INT_MAX)
{
dist[j]=S[1][j];
from[j]=1;
}
}
for(j=2;j<N+1;j++)
{
for(i=2;i<j;i++)
{
if(S[i][j]<INT_MAX)
{
if(dist[i]+S[i][j]<dist[j])
{
dist[j]=dist[i]+S[i][j];
from[j]=i;
}
}
}
}
cout<<"最短路径为:";
i=6;
cout<<N<<" "<<from[i]<<" ";
i=from[i];
while(i!=1)
{
cout<<from[i]<<" ";
i=from[i];
}
cout<<"\n";
cout<<"最短距离为:"<<dist[N]<<endl;
}
int main()
{
int N;
int **S,*dist,*from;
int i,j;
cout<<"输入点的个数:";
cin>>N;
S=new int*[N+1];
for(i=0;i<N+1;i++)
{
S[i]=new int[N+1];
for(j=0;j<N+1;j++)
{
S[i][j]=INT_MAX;
}
}
dist=new int[N+1];
for(i=0;i<N+1;i++)
{
dist[i]=INT_MAX;
}
from=new int[N+1];
for(i=0;i<N+1;i++)
{
from[i]=0;
}
Init_Graph(N,S);
DP(N,S,dist,from);
for(i=0;i<N+1;i++)
{
delete []S[i];
}
delete []S;
delete []dist;
delete []from;
return 0;
}
算法概论实验五
1 | 实验五 |
#LIS Question
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75// test5.1.cpp :
// 1.最长递增子序列问题
//【问题描述】
//给定一个整数数组,设计一个动态规划算法求出该数组中的最长递增子序列。
//
#include "stdafx.h"
#include <iostream>
using namespace std;
// 输出LIS 序列
void outputLIS(int * arr, int index, int lis, int *L)
{
//终止条件
if (lis == 0 || index < 0)
return;
//找到第一个L[index]==lis
while (L[index]!=lis && index>0)
index--;
//反序输出
if (index >= 0 && L[index]==lis)
{
outputLIS(arr, index - 1, lis - 1, L);
cout << arr[index] << ",";
}
}
int LIS(int *a, int n)
{
//定义一个存取结果的数组
int *L = new int[n];
//填写次序 0 to n-1
for (int j = 0; j < n;j++)
{
L[j] = 1;//BaseCase
//find max L[i]
for (int i = 0; i < j;i++)
{
if (a[i]<a[j] && L[i]+1 > L[j])
{
L[j] = L[i] + 1;
}
}
}
//return the max of L[0~n-1]
int max = L[0];
for (int i = 0; i < n; i++)
{
//cout << L[i] << " ";
if (L[i]>max)
{
max = L[i];
}
}
//回溯输出
cout << "LIS如下:";
outputLIS(a, n,max, L);
return max;
}
int main()
{
int a[] = { 5, 2, 8, 6, 3, 6, 9, 7, };
int n = sizeof(a) / sizeof(int);
cout<<endl<<"长度为:" << LIS(a, n) << endl;
return 0;
}
#矩阵连乘1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65#include<iostream>
#include<vector>
using namespace std;
vector<int> save;
void getalise(int *v,int n);
void main()
{
int a[7]={3,4,52,13,8,1,6};
getalise(a,7);
}
int Max(int a,int b)
{
return a>b?a:b;
}
void getalise(int *v,int n)
{
int *pre=new int[n];
int *max=new int[n];
for (int i = 0; i < n; i++)
{
max[i]=1;
pre[i]=-1;
}
vector<int> *sta= new vector<int>[n];
for (int i = 0; i < n-1; i++)
{
for (int j = i+1; j < n; j++)
{
if (v[i]<v[j])
{
sta[i].push_back(j);
}
}
}
for (int i = n-1; i >=0 ; i--)
{
for (int j = 0; j < sta[i].size(); j++)
{
max[i]=Max(max[i],1+max[sta[i].at(j)]);
if (max[i]==1+max[sta[i].at(j)])
{
pre[i]=sta[i].at(j);
}
}
}
int idmax=0;
int temp=-1;
for (int i = 0; i < n; i++)
{
if (temp<max[i])
{
idmax=i;
temp=max[i];
}
}
while (pre[idmax]!=-1)
{
cout<<v[idmax]<<" ";
idmax=pre[idmax];
}
cout<<v[idmax];
delete []pre;
delete []max;
delete []sta;
}
算法概论实验六
1 | 实验六 |
##The LCS Question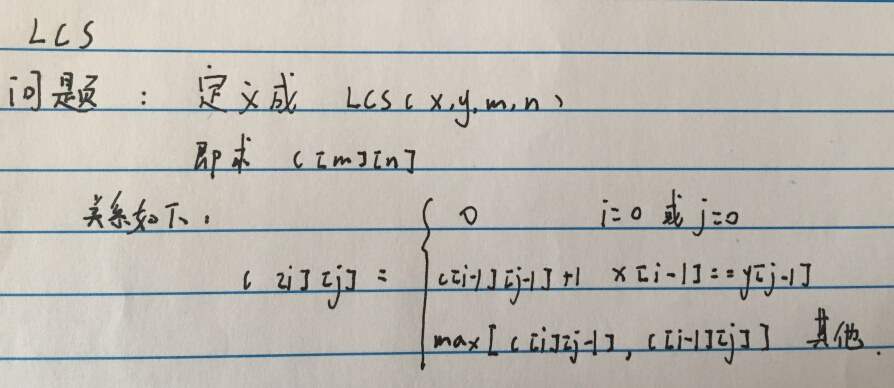
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93// ConsoleApplication2.cpp : 定义控制台应用程序的入口点。
// VS2013 CPP CODE
//
#include "stdafx.h"
#include<iostream>
using namespace std;
void PrintLcsPath(int ** b, char * x, int m, int n)
{
if (m == 0 | n == 0)
return;
if (b[m][n] == 1)
{
PrintLcsPath(b, x, m - 1, n - 1);
cout << x[m - 1];
}
else if (b[m][n] == 2)
PrintLcsPath(b, x, m, n - 1);
else
PrintLcsPath(b, x, m - 1, n);
}
void print(int ** a, int m, int n)
{
for (int i = 0; i < m + 1; i++)
{
for (int j = 0; j < n + 1; j++)
cout << a[i][j] << " ";
cout << endl;
}
}
int LcsLength(char *x, char *y, int m, int n)
{
//创建一个 m+1 * n+1 用于存储LCS
int **a = new int *[m + 1];
for (int i = 0; i < m + 1; i++)
a[i] = new int[n + 1];
//创建一个 m+1 * n+1 用于存储状态
//来自于对角线 1 来自于左侧2 来自于上方3
int **b = new int *[m + 1];
for (int i = 0; i < m + 1; i++)
b[i] = new int[n + 1];
//base case
for (int i = 0; i < m + 1; i++)
a[i][0] = 0;
for (int i = 0; i < n + 1; i++)
a[0][i] = 0;
//for
for (int i =1; i < m + 1;i++)
{
for (int j =1; j < n + 1;j++)
{
if (x[i-1]==y[j-1])
{
a[i][j] = a[i - 1][j - 1] + 1;
b[i][j] = 1;
}
else
{
if (a[i-1][j] <= a[i][j-1])
{
a[i][j] = a[i][j - 1];
b[i][j] = 2;
}
else
{
a[i][j] = a[i - 1][j];
b[i][j] = 3;
}
}
}
}
/*print(a, m, n);
cout << endl;
print(b, m, n);*/
cout << "LCS为:";
PrintLcsPath(b, x, m, n);
cout << endl;
return a[m][n];
}
int main()
{
char x[] = "12312312qwe12312";
char y[] = "abqweqw123e123123qwcbdab";
int m = strlen(x);
int n = strlen(y);
cout << "LCS的长度为:" << LcsLength(x, y, m, n) << endl;
}
##0-1背包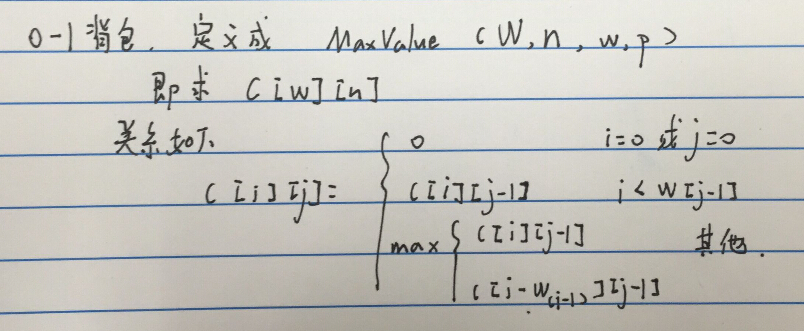
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92// N给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为W(假定物品重量与背包容量值均为整数),应如何选择装入背包中的物品,使得装入背包中物品的总价值最大?设计一个动态规划算法,求解背包问题。
//
#include "stdafx.h"
#include <iostream>
using namespace std;
#define W 50
void print(int ** a, int m, int n)
{
for (int i = 0; i < m + 1; i++)
{
for (int j = 0; j < n + 1; j++)
cout << a[i][j] << " ";
cout << endl;
}
}
void Trackback(int *weight, int n, int w,bool *p,int **a)
{
if (n==0 || w==0)
return;
if (a[w][n]==a[w][n-1])//若和左边的一致,说明没有选最后一个
{
p[n - 1] = false;
Trackback(weight, n - 1, w, p, a);
}
else
{
p[n - 1] = true;
Trackback(weight, n - 1, w-weight[n-1], p, a);
}
}
int getMaxValue(int w, int n, int *price, int * weight )
{
//创建一个 w+1 * n+1 的二维表
int **a = new int *[w + 1];
for (int i = 0; i < w + 1;i++)
{
a[i] = new int[n + 1];
}
//创建一个数组 记录货物是否取的状态
bool *p = new bool[w];
memset(p, false, sizeof(p));
//base case
for (int i = 0; i < w + 1; i++)
a[i][0] = 0;
for (int i = 0; i < n + 1; i++)
a[0][i] = 0;
//for
for (int i = 1; i < w + 1;i++)
{
for (int j = 1; j < n + 1;j++)
{
if (i<weight[j-1])//填写a[i][j],若当前背包重量小于物品,则不装
{
a[i][j] = a[i][j - 1];
}
else
{
if (a[i][j-1] <= a[i-weight[j-1]][j-1]+price[j-1])
{
a[i][j] = a[i - weight[j - 1]][j - 1] + price[j - 1] ;
}
else
a[i][j] = a[i][j - 1];
}
}
}
//print(a,w,n);
Trackback(weight, n, w, p, a);
cout << "从左到右是否取件为:";
for (int i = 0; i < n; i++)
cout << p[i] << " ";
cout << endl;
return a[w][n];
}
int main()
{
//int price[] = { 1, 2, 3, 4, 7 };
//int weight[] = { 2, 4, 5, 6, 210 };
int price[] = { 60, 100, 120 };
int weight[] = { 10, 20, 30 };
cout << "背包问题的解是:"<<getMaxValue(W, 5, price, weight) << endl;
return 0;
}
算法概论实验七
1 | 实验七 |
1 | #include <iostream> |
算法概论实验八
1 | 实验八 |
#贪心法迭代
1 | #include "stdafx.h" |
#贪心法 递归
每次递归,将问题的规模减少1~n,1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24#include "stdafx.h"
#include <iostream>
using namespace std;
//i是上一个符合条件的id,为了完整性,在第一列加上-1,n是总数目
void GetSet(int *si, int *fi, int i, int n)
{
int m = i + 1;
while (m <= n && si[m] < fi[i])//找第一个符合的
m = m + 1;
if (m <= n)
{
cout << m << "\t";
GetSet(si, fi, m, n);
}
}
int main()
{
int si[] = { -1,1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12 };
int fi[] = { -1,4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 };
int n = 11;
GetSet(si, fi, 0, 11);
}
#1001 Sum Problem1
In this problem, your task is to calculate SUM(n) = 1 + 2 + 3 + ... + n
1 | #include<stdio.h> |
#1002 A + B Problem II1
大数相加 cpp
1 | #include<cstdio> |
#1003 Max Sum1
最大连续子段和 cpp
1 | #include <iostream> |
#1004 Let the Balloon Rise1
找出出现最多的颜色 cpp
1 | #include <iostream> |
#1005 Number Sequence1
f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.
1 | #include<stdio.h> |
#1007Quoit Design1
求任两点间距离最小的两点间的距离
1 | #include <iostream> |
#1008 电梯问题1
2花费6秒移动电梯一层,4秒移动到下一层。电梯将在每一站停留5秒。
3 2 3 1 === 41s
1 | #include <stdio.h> |
#1
2老鼠有很多的猫粮 要和看仓库的猫换java豆吃 每个仓库的java豆有不同的储量和价格
老鼠想你帮助他用自己猫粮换最多的java豆
1 | #include<stdio.h> |
#1024 dp 最大M籽椴和1
2
3
4
5
6
7
8
9
10
11
12问题:
给定由n个整数(可能为负整数)组成的序列e1,e2,…,en,以及一个正整数m,要求确定序列的m个不相交子段,使这m个子段的总和达到最大。
分析:
设b(i,j)表示数组e的前j项中i个子段和的最大值,且第i个子段含e[j](1£ i £m,i£ j £n)。以下称b(i, j)为“最后一个元素属于第i子段的j元素i子段问题”。则n个元素中求i个子段的最优值显然为:
best(i, n) = Max{ b(i, j) } (i <= j <= n)
计算b(i,j)的最优子结构为:
b(i,j) = Max{ b(i, j-1) + e[i], Max{ b(i-1, t) } + e[i] } (i <= t < j)
这样,可以得到时间复杂度为O(m * n ^ 2)和空间复杂度为O(m * n)的MS相当漂亮而且容易理解的DP算法。当n不大的时候,这个算法足够优秀,然而,当n很大的时候,这个算法显然是不能让人满意的!
优化:
观察上面的最优子结构,我们发现b(i, j)的计算只和b(i, j-1)和b(i-1, t)有关,也就是说只和最后一个元素属于第i子段的j-1元素i子段问题和前j-1个元素的最大i-1子段问题有关(可以分别理解为将e[j]作为最后一个元素而并入第i子段和将e[j]另起一段作为第i分段)。这样,我们只要分别用curr_best和prev_best两个一维数组保存当前阶段和前一阶段的状态值b(i, *)和b(i-1, *) 就行了,内存使用也就可以降为O(2 * n)。
再来看看时间。分析发现,原算法低效主要是在求max_sum(i, t) = Max{b(i, t)} (i <= t < j)的时候用了O(n)的时间。其实,在求b(i, j)的过程中,我们完全可以同时计算出max_sum(i, t),因为max_sum(i,j) = Max{b(i,j), max_sum(i,j-1)},这个只花费O(1)的时间。而max_sum(i,t)不就是i+1阶段中要用到的吗?关键问题已经解决了!那如何保存max_sum呢?再开一个数组?我们可以在prev_best数组中保存!这个数组的任务相当艰巨,它既存放着i-1阶段的max_sum数值,又存放这供i+1阶段使用的i阶段的max_sum值。MS这有点矛盾?其实这是可行的。注意到我们在计算b(i,j)时只使用了prev_best[j-1],使用完了再也没有用了,这样空闲着岂不浪费?其实我们可以将max_sum(i, j-1)存放到prev_best[j-1]里面——这个主意相当不错,它让所有问题迎刃而解。
现在,我们得到了一个时间复杂度为O(m * n)、空间复杂度为(2 * n)的算法。这个算法相当优秀,以至于m为小常数,n = 1000000时,结果也是瞬间就出来了(此时算法的时间复杂度可以认为是O(n)的)。
1 | #include<stdio.h> |