利用状态空间法解决八数码游戏问题

---

学号： 19130216
姓名： 陈实
完成时间：2015年11月24日

---

#1.八数码游戏简介

八数码问题也称为九宫问题。在3×3的棋盘，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格，与空格相邻的棋子可以移到空格中。
要求解决的问题是：给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。
所谓问题的一个状态就是棋子在棋盘上的一种摆法。解八数码问题实际上就是找出从初始状态到达目标状态所经过的一系列中间过渡状态。

---

#2.八数码游戏问题的状态空间法表示

（利用课程介绍的状态空间法来描述八数码游戏问题，需定义相应的状态与操作符）

---

##2.1.状态定义
利用矩阵存储每一步的状态，空位用0表示，例如：
初始状态为
\begin{equation} %开始数学环境
\left( %左括号
\begin{array}{ccc} %该矩阵一共3列，每一列都居中放置
2 & 8 & 3\ %第一行元素
1 & 0 & 4\ %第二行元素
7 & 6 & 5
\end{array}
\right) %右括号
\end{equation}
目标状态为
\begin{equation} %开始数学环境
\left( %左括号
\begin{array}{ccc} %该矩阵一共3列，每一列都居中放置
1 & 2 & 3\ %第一行元素
8 & 0 & 4\ %第二行元素
7 & 6 & 5
\end{array}
\right) %右括号
\end{equation}
将所有的中间生成状态列成图表，可以清晰的看出搜索的顺序，直观地理解算法。

---

##2.2.定义算符

• 空格的上、下、左、右移动

并标记为四个方向的箭头如下图所示：

---

##2.3.从初始状态到目标状态的求解过程
例：下图为宽度优先搜索算法对应具体搜索路径：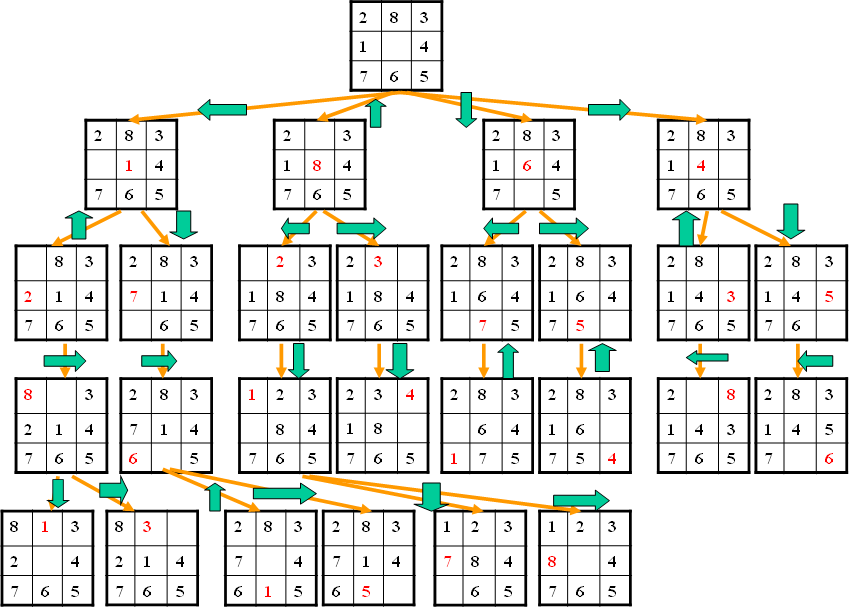

---

#3.八数码游戏问题的盲目搜索技术概述

（介绍宽度和深度优先搜索算法的基本原理和流程图）
（算法复杂性分析：时间与空间复杂性（选做））

---

##3.1.宽度优先搜索算法

###3.11.宽度优先搜索定义

• 宽度优先搜索：以接近起始节点的程度依次扩展节点的搜索技术（即：离起始节点近的节点先被扩展）
• 扩展节点的原则：先扩展出来的节点随后优先被扩展（生成其所有的后继节点）

---

###3.12.宽度优先搜索算法步骤

• ① 把起始节点放到 OPEN 表中(如果该起始节点为一目标节点，则得到解)
• ② 如果 OPEN 是个空表，则无解，失败退出；否则继续下一步
• ③ 把第一个节点(记作节点 n )从 OPEN 表移出，并把它放入 CLOSED 的已扩展节点表中
• ④ 扩展节点 n 。如果没有后继节点，则转向第②步
• ⑤ 把 n 的所有后继节点放到OPEN表的末端，并提供从这些后继节点回到 n 的指针(记录每一个节点的父节点信息)
• ⑥ 如果 n 的任一个后继节点是个目标节点，则找到一个解（反向追踪得到从目标节点到起始节点的路径），成功退出，否则转向第②步

---

###3.13.宽度优先搜索算法的流程图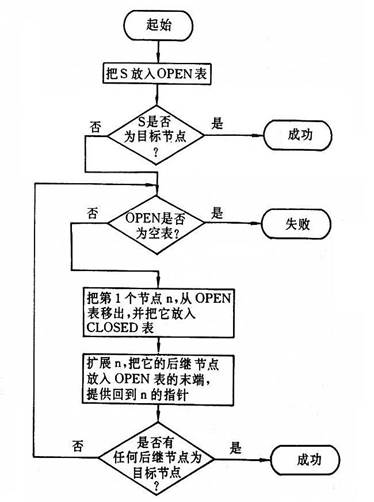

---

##3.2.深度优先搜索算法

###3.21.深度优先搜索定义
深度优先搜索过程是沿着一条路径进行下去，直到深度界限为止，然后再考虑只有最后一步有差别的相同深度或较浅深度可供选择的路径，接着再考虑最后两步有差别的那些路径。

• 深度优先搜索策略是先扩展最新产生的(即最深的)节点
• 深度优先搜索的基本思路：先扩展最深的节点。当出现没有后继节点时，换到旁边的次深节点

---

###3.22.深度优先搜索算法步骤

• ① 把起始节点 S 放到未扩展节点的 OPEN 表（此时OPEN表是一个堆栈，后进先出）中。如果此节点为一目标节点，则得到解
• ② 如果 OPEN 为一空表，则无解、失败退出
• ③ 把第一个节点(记作节点 n )从 OPEN 表移到 CLOSED 表
• ④ 如果节点 n 的深度等于最大深度，则转向②
• ⑤ 扩展节点 n ，产生其全部后继节点，并把它们放入 OPEN 表的前头。如果没有后继节点，则转向②
• ⑥ 如果后继节点中有任一个节点为目标节点，则求得一个解（反向追踪从目标节点到起始节点的路径），成功退出；否则，转向②

---

###3.23.深度优先搜索算法的流程图

---

#4.八数码游戏问题的启发式搜索技术

（给出你所采用估价函数，并介绍算法的基本原理和流程图）

##4.1.启发式搜索原理

• 启发信息：与具体问题特性有关的一些信息。（在具体的使用过程中，还与使用人、算法有关）
• 启发式搜索方法：利用启发信息的搜索方法

启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径，提高了效率。在启发式搜索中，对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。

---

##4.2.估价函数
估价函是用来估算节点“ 希望 ”程度的函数

• 一般情况下，估计函数值越大，希望程度就越低
• 根据搜索过程、问题的启发信息来定义的，对搜索效率会产生较大的影响
• 用 f (n) 表示节点 n 的估价函数值，并且期望，它是从起始节点、通过节点 n 、到达目标节点的最小代价的一个估计值

---

##4.3.估价函数的计算
计算一个节点的“ 估价函数 ” ，可以分成两个部分：

• ①已经付出的代价（起始节点到当前节点）
• ②将要付出的代价（当前节点到目标节点）
• 节点 n 的估价函数 $f ( n )$ 定义为从初始节点、经过 n到达目标节点的路径的最小代价的估计值，即$f(n)=g(n)+h(n)$
• $g ( n )$ 是从初始节点到达当前节点 n 的实际代价
• $h ( n )$ 是从节点 n 到目标节点的最佳路径的估计代价

$h ( n )$ 体现出搜索过程中采用的启发式信息（背景知识），称之为启发函数
$g ( n )$ 所占的比重越大，越趋向于宽度优先或等代价搜索；
$h ( n )$ 的比重越大，表示启发性能就越强

---

##4.4. 有序搜索算法
在搜索过程中，OPEN表中节点按照其估价函数值以递增顺序排列，选择OPEN表中具有最小估价函数值的节点作为下一个待扩展的节点，这种搜索方法称为有序搜索。

---

##4.5. 算法描述

• ① 把起始节点S放到OPEN表中，并计算节点S的$f (S)$；
• ② 如果OPEN是空表，则失败退出（无解）；
• ③ 从OPEN表中选择一个f值最小的节点i。如果有几个节点值相同，当其中 有一个为目标节点时，则选择目标节点；否则就选择其中任一个节点作为节点i；
• ④ 把节点 i 从 OPEN 表中移出，并把它放入 CLOSED 的已扩展节点表中
• ⑤ 如果 i 是个目标节点，则成功退出（有解）
• ⑥ 扩展节点 i ，生成其全部后继节点。对于 i 的每一个后继节点 j ：
• ⑦ 转向②

---

##4.6.算法流程图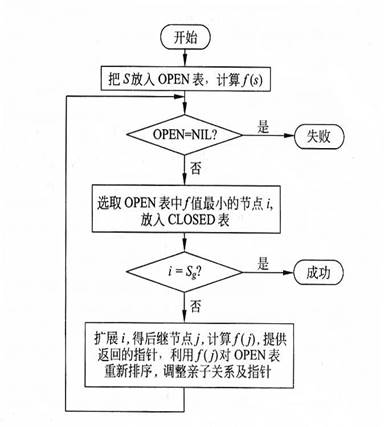

---

#5.例子及分析

对于算法的运行过程，需要记录下列信息：
起始状态、目标状态、所走的步数及其对应操作符、生成的状态总数（OPEN表和CLOSED表的大小）、搜索CPU时间（毫秒）等。

##5.1.测试例子1
初始状态：
\begin{equation} %开始数学环境
\left( %左括号
\begin{array}{ccc} %该矩阵一共3列，每一列都居中放置
2 & 0 & 3\ %第一行元素
1 & 8 & 4\ %第二行元素
7 & 6 & 5
\end{array}
\right) %右括号
\end{equation}
目标状态：
\begin{equation} %开始数学环境
\left( %左括号
\begin{array}{ccc} %该矩阵一共3列，每一列都居中放置
1 & 2 & 3\ %第一行元素
8 & 0 & 4\ %第二行元素
7 & 6 & 5
\end{array}
\right) %右括号
\end{equation}

###运行截图

####宽度优先搜索：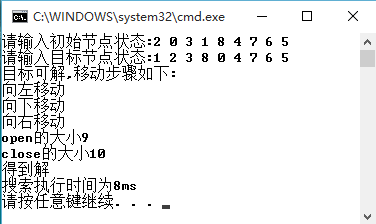

####深度优先搜索：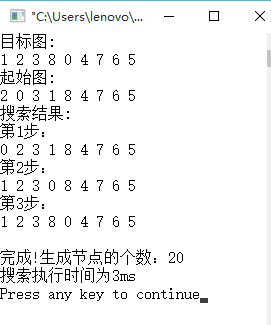

####启发式搜索：

| 项目 | 宽度优先搜索 | 深度优先搜索|启发式搜索
|—| —– |
|起始状态|2 0 3 1 8 4 7 6 5|2 0 3 1 8 4 7 6 5|2 0 3 1 8 4 7 6 5|
|目标状态|1 2 3 8 0 4 7 6 5|1 2 3 8 0 4 7 6 5|1 2 3 8 0 4 7 6 5|
|所走的步数|3|3|3
|对应操作符|L D R|L D R|L D R
|生成的状态总数|10|20|3
|搜索CPU时间|8ms|3ms|0ms

---

##5.2.测试例子2
初始状态：
\begin{equation} %开始数学环境
\left( %左括号
\begin{array}{ccc} %该矩阵一共3列，每一列都居中放置
2 & 8 & 3\ %第一行元素
1 & 6 & 4\ %第二行元素
7 & 0 & 5
\end{array}
\right) %右括号
\end{equation}
目标状态：
\begin{equation} %开始数学环境
\left( %左括号
\begin{array}{ccc} %该矩阵一共3列，每一列都居中放置
1 & 2 & 3\ %第一行元素
8 & 0 & 4\ %第二行元素
7 & 6 & 5
\end{array}
\right) %右括号
\end{equation}

###运行截图

####宽度优先搜索：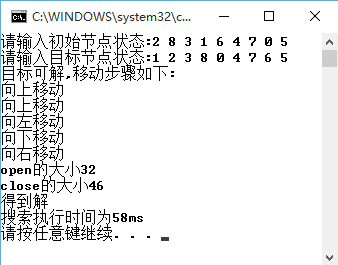

####深度优先搜索：

####启发式搜索:

| 项目 | 宽度优先搜索 | 深度优先搜索|启发式搜索
|—| —– |
|起始状态|2 8 3 1 6 4 7 0 5|2 8 3 1 6 4 7 0 5|2 8 3 1 6 4 7 0 5
|目标状态|1 2 3 8 0 4 7 6 5|1 2 3 8 0 4 7 6 5|1 2 3 8 0 4 7 6 5
|所走的步数|5|5|5
|对应操作符| U U L D R|U U L D R|U U L D R
|生成的状态总数|46|121|5
|搜索CPU时间|58ms|4ms|0ms

---

#6．体会与致谢

（说一说，做这一编程实验与书写报告的体会。如果求助过同学，请在此表示感谢）

通过本次试验，我对BFS、DFS以及启发式搜索有了更加深入的了解。同时感谢老师课上的指导，以及课程PPT的制作，对我作业的编写有很大的帮助。下面说说我的想法：

• 在试验中，通过用不同的测试数据结果来看，宽度优先搜索方法能够保证在搜索树中找到一条通向目标节点的最短途径（所用操作符最少），只要结点间可以到达，就一定可以找到一个最优解。
• 而深度优先搜索具有深度界限，当搜索深度达到深度界限时，停止搜索。所以，深度优先搜索有可能会得不到结果，是一种不安全的搜索方法。但是当结果在搜索界限内时，可以快速的得到结果，时间效率高。故对于深度优先搜索，如何去定义一个较好的搜索界限，是下一步需要继续改进的方面。
• 相比之下，启发式搜索看来更加实用有效，能在较复杂情况下求得更加优质的解，但是对于估价函数的定义趋向多元化，如何更好地定义一个估价函数有待深入讨论。

---

#7．实验程序简单说明

（简要地说明实验程序的使用方法，此处不用附源代码）

三段程序均仅需要输入初始状态和目标状态即可

• 宽度优先会提供操作符的方向
• 深度优先会输出第一个能够找到解的宽度
• 启发式搜索具有更加实用的效率

---

##代码介绍：

###7.1.宽度优先搜索

/*定义状态结构*/
class NineNode{……}；

/*判断两个节点是否相同，相同返回true，否则返回false*/
bool match(NineNode node1, NineNode node2)  

/*判断新节点是否已经存在，即判断是否存在于open队列和closed列表中*/
bool ishave(deque<NineNode> openQueue, vector<NineNode> closedList, NineNode node)

/*判断给定的八数码问题是否有解*/
bool havesolution(NineNode start, NineNode end)

/*用于状态的输入和状态的选择*/
int main()

###7.2.深度优先搜索

//定义结构
struct Map{……}；

//打印图
void PrintMap(struct Map *map);

//移动图
struct Map * MoveMap(struct Map * map, Direction Direct, bool CreateNewMap);

//初始化一个初始图,由目标图生成初始图，保证可以获得结果
struct Map * RandomMap(const struct Map * map);

//初始图的另种生成方式，随机生成各位置的数,此方式生成的图在有限次搜索中若深度超过5则多数无解
struct Map * RandomMap();

//判断是否搜索成功
bool IsSuccess(struct Map * map, struct Map * Target);

//深搜过程
struct Map * DNF_Search(struct Map * begin, struct Map * Target, int dm)

###7.3.启发式搜索

//定义存储结构
struct node{……};

//函数说明：计算s与目标状态的差距值
int hx(int s[3][3])；

//函数说明：扩展ex指向的结点，并将扩展所得结点组成一条单链表，head指向该链表首结点，并且作为返回值
struct node *extend(node *ex)； 
	
//函数说明：将head链表的结点依次插入到open链表相应的位置，使open表中的结点按从小到大排序。函数返回open指针
node* insert(node *open, node * head)；
	
//状态的输入和状态的选择
int main()

---

完成时间 2015年11月24日